Asymmetric Loss For Multi-Label Classification
이번 시간에는 Imbalance Dataset에 좋은 성능을 보여주는 Asymmetric Loss(이하 ASL)에 대해서 공부한 내용을 정리해보고자 한다.
논문 개요
- Asymmetric Loss를 이용하여 Multi-Label에 필연적으로 따라오는 Positive Label과 Negative Label의 Imbalance문제와 mislabeling 문제를 해결 가능하다.
- 기존 아키텍쳐를 변형하는게 아닌 Loss만을 이용하기 때문에 도입하기 쉽고, 추가적인 학습시간 등의 부하 없이 성능을 상승시킬수 있다.
Binary Cross-Entropy and Focal Loss
우선 ASL에 들어가기 앞서 Multi Label Loss의 기본이 되는 Binary Cross Entropy(이하 BCE)와 Imbalance에 맞추어 설계된 Focal Loss에 관하여 Positive와 Negative를 나누어 생각을 해보자. 이렇게 나누는 이유는 본 글의 주제인 Asymmetric Loss가 Positive, Negative를 나누어 비대칭적으로 설계했기 때문에 그 차이를 비교해보기 위해서다.
우선 두 Loss 함수 공통적으로 전체 클래스에 관한 손실함수 $L_{tot}$는 아래와 같이 정의가 가능하다.
- $\sigma$ : sigmoid 함수
- $z_{k}$, $y_{k}$ : 클래스 $k$에 대한 예측, 라벨값
- $L$ : 각각의 Loss
$$ L_{tot} = \sum_{k=1}^{K}L(\sigma (z_{k}), y_{k}) $$
여기서 $L$을 일반적으로 나타내면 아래와 같다.
$$ L = -yL_{+} - (1-y)L_{-} $$
BCE일 경우 L은 Cross Entropy의 형태를 띄고 Focal Loss일 경우 아래와 같은 방식을 취하게 된다.
$$ \begin{align} L_{+} &= (1-p)^{\gamma} \log (p) \\ L_{-} &= p^{\gamma} \log (1-p) \end{align} $$
여기서 $\gamma$는 focusing parameter 이며 값을 크게할 수록 Easy negative 에 대해서 Loss function을 낮게 가져갈 수 있게되고, 좀더 어려운 Sample에 대해서 집중할 수 있게 된다고 한다.
Asymmetric Loss
Focal Loss는 기본적으로 단일 Classification에 맞추어 설계되어있기 때문에 Multi Label에 적용할 경우 아래와 같은 문제가 발생 할 수 있다고 논문에서 서술하고 있다.
When using focal loss for multi-label training, there is an inner trade-off: setting high γ, to sufficiently down-weight the contribution from easy negatives, may eliminate the gradients from the rare positive samples.
$\gamma$ 값이 클 경우 easy negatives 의 영향을 줄일수 있지만, rare한 Positive Sample의 gradient 또한 소실 될 수 있다는 부분이다. 이러한 부분을 해결하기 위해서 Asymmetric Loss에서는 우선 Asymmetric Focusing이라는 기법을 통하여 Loss를 다시 디자인 했다.
Asymmetric Focusing
Asymmetric Focusing은 위의 Focal Loss에서 사용된 Focusing Parameter를 비대칭적으로 설계하여 Positive와 Negative의 가중치를 다르게 주는 설계를 말한다.
$$ \begin{align} L_{+} &= (1-p)^{\gamma + } \log (p) \\ L_{-} &= p^{\gamma - } \log (1-p) \end{align} $$
Asymmetric Focusing을 적용한 식은 Focal Loss와 거의 비슷하지만, focusing paramter $\gamma$가 $\gamma +$ 와 $\gamma - $ 로 나뉜것을 볼 수 있다. $\gamma +$ 와 $\gamma - $ 는 항상 $\gamma - > \gamma +$로 설정하여 위에서 이야기 했던 rare positive examples의 소실을 방지 시킬 수 있게 된다.
Asymmetric Probability Shifting
위의 Asymmetirc Focusing을 적용하여 Negative Sample에 대해서 많은 패널티를 주었지만 극단적인 Imbalance 상황을 가정 할 때 이는 충분하지 않을 수 있다. 그래서 추가적으로 negative sample에 대해서 probability가 일정 값 이하일 경우 0으로 만들어 버리는 hard threshold 인 asymmetric probability shifting을 적용한다.
- $m$ : margin, p가 이 값보다 작으면 0으로 만들어주는 기준값
$$ p_{m} = max(p-m, 0) $$
이에 negative loss $L_{-} 는 아래와 같이 적용된다.
$$ L_{-} = (p_{m})^{\gamma} \log (1-p_{m}) $$
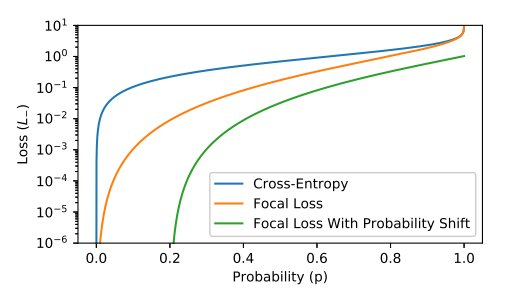
ASL Definition
위에서 이야기한 Asymmetric focusing과 Asymmetric probability shifting를 둘다 적용하여 ASL Loss를 나타낼 수 있다.
$$ \begin{align} L_{+} &= (1-p)^{\gamma + } \log (p) \\ L_{-} &= (p_{m})^{\gamma -} \log (1-p_{m}) \end{align} $$